LeetCode 412. Maximum XOR of Two Numbers in an Array 的Trie树加分治法解法

题目原文

421. Maximum XOR of Two Numbers in an Array

Difficulty: Medium

Given a non-empty array of numbers, a₀, a₁, a₂, … , a_n-1, where 0 ≤ a_i < 2³¹.

Find the maximum result of a_i XOR a_j, where 0 ≤ i, j < n.

Could you do this in O(n) runtime?

Example:

Input: [3, 10, 5, 25, 2, 8]

Output: 28

Explanation: The maximum result is 5 ^ 25 = 28.

解法：使用 Trie 树（前缀树）和分治法

时间复杂度 O(n)

根据题目描述，我们需要找到最大的异或值，异或代表了两个数的二进制的不同程度，且越高位越不一样，异或值就越大，由于是按位比较，所以使用 Trie 树来当做基础数据结构。

我们可以总结出以下几点：

1. 因为整型的位数是固定的，排除第一位符号位，Trie 树的高度是常数的，即最高32层（包括root）
2. 由于只有0和1两个子节点，所以为了节省空间，可以使用二叉树的方式（或者数组和 HashMap 均可）
3. 由于是异或，前缀位如果相同，异或值都是 0，所以可以先找到第一个两个子节点都不为空的节点当做root

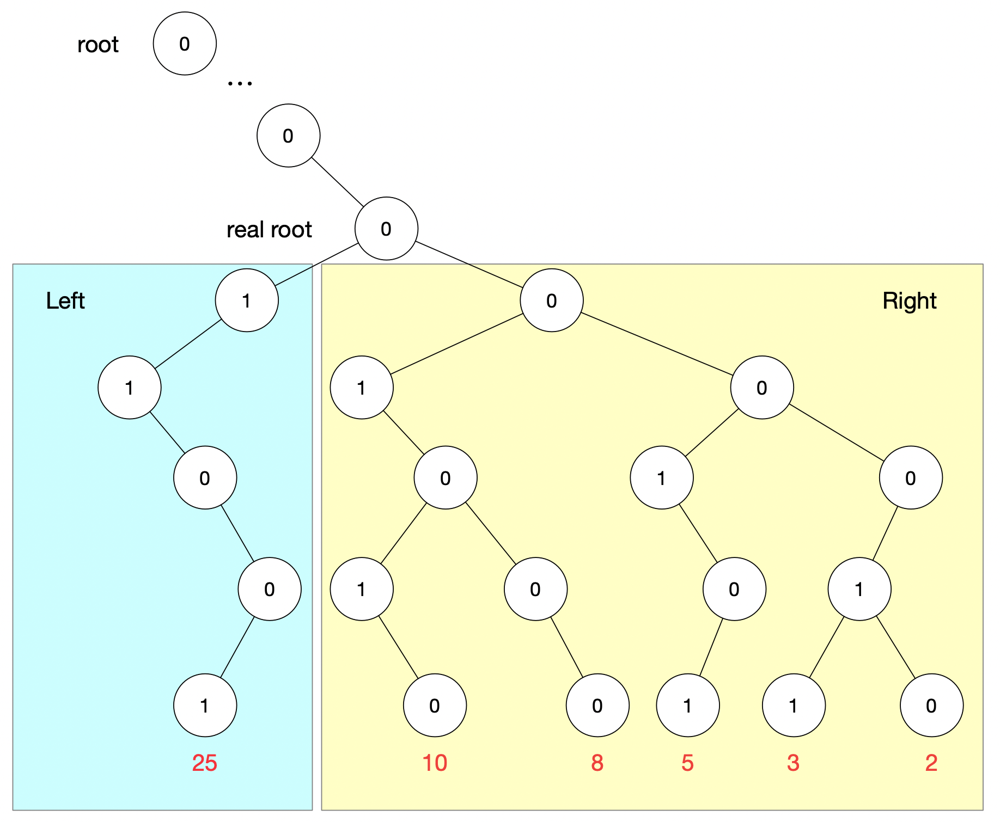
以此构建 Trie 树，代码如下：

class Solution {
    class TrieNode {
        int val;
        TrieNode zero, one;
        boolean isEnd;
    }
    class TrieTree {
        TrieNode root;
        public TrieTree() {
            root = new TrieNode();
        }
        public void insert(int num) {
            TrieNode cur = root;
            int j = 1 << 30;
            for (int i = 0; i < 31; i++) {
                // 根据num在j位置的数目判断应该向0还是向1
                int b = (j & num) == 0 ? 0 : 1;
                if (b == 0 && cur.zero == null) {
                    cur.zero = new TrieNode();
                }
                if (b == 1 && cur.one == null) {
                    cur.one = new TrieNode();
                }
                cur = b == 0 ? cur.zero : cur.one;
                j >>= 1;
            }
            cur.isEnd = true;
            cur.val = num;
        }
    }

    public int findMaximumXOR(int[] nums) {
        if (nums == null || nums.length <= 1) {
            return 0;
        }
        TrieTree tree = new TrieTree();
        for (int n : nums) {
            tree.insert(n);
        }
        // 获取真正需要开始判断的root
        TrieNode cur = tree.root;
        while (cur.one == null || cur.zero == null) {
            cur = cur.zero != null ? cur.zero : cur.one;
        }
        return maxHelper(cur.one, cur.zero);

    }

    /**
     * 分治法，原则就是尽量使两个分支的高位不同
     * one是1分支，zero是0分支，可以看做图中的左区和右区
     * 1. 当1分支的下一位只有1时，找0分支的0，若没有，就找0分支的1
     * 2. 当1分支的下一位只有0时，找0分支的1，若没有，就找0分支的0
     * 3. 当1分支的下一位0，1均有时，看0分支：如果0分支只有1，则1分支走0，反之则走1
     * 4. 当0，1两个分支均有两个下一位时，尝试【1分支走1，0分支走0】和【1分支走0，0分支走1】两条路线并取最大值
     * */
    private int maxHelper(TrieNode one, TrieNode zero) {
        if (one.isEnd && zero.isEnd) {
            return one.val ^ zero.val;
        }
        if (one.zero == null) {
            return maxHelper(one.one, zero.zero == null ? zero.one : zero.zero);
        } else if (one.one == null) {
            return maxHelper(one.zero, zero.one == null ? zero.zero : zero.one);
        } else if (zero.zero == null) {
            return maxHelper(one.zero, zero.one);
        } else if (zero.one == null) {
            return maxHelper(one.one, zero.zero);
        } else {
            return Math.max(maxHelper(one.one, zero.zero), maxHelper(one.zero, zero.one));
        }
    }
}

本文同样发在了 LeetCode 讨论区